Question

A random sample of 300 Americans planning long summer vacations in 2009 revealed an average planned expenditure of $1,076. The expenditure for all Americans planning long summer vacations has a normal distribution with a standard deviation 345. Give a 99% confidence interval for the mean planned expenditure by all Americans taking long summer vacations in 2009. Explain your answer in relation to this context.

Answer 1

`(1024.69,\ 1127.31)`

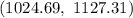
Explanation:

We know that the sample size was:

`n = 300`

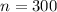
The average was:

`{\displaystyle {\overline {x}}}=1,076`

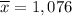
The standard deviation was:

`\s = 345`

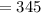
The confidence level is

`1-\alpha = 0.99`

`\alpha=1-0.99\\\alpha=0.01`

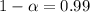
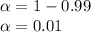
The confidence interval for the mean is:

`{\displaystyle{\overline {x}}} \± Z_{(\alpha)/(2)}*(s)/(√(n))`

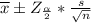
Looking at the normal table we have to

`Z_{(\alpha)/(2)}=Z_{(0.01)/(2)}=Z_(0.005)=2.576`

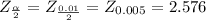
Therefore the confidence interval for the mean is:

`1,076\± 2.576*(345)/(√(300))`

`1,076\± 51.31`

`(1024.69,\ 1127.31)`

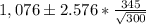
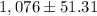
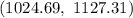
This means that the mean planned spending of all Americans who take long summer vacations in 2009 is between $ 1024.69 and $ 1127.31