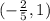Answer:
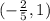
Explanation:
The problem is based on Section Formula which is given as under
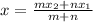
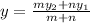
Where the m and n are the ratio in which the point
![P(x,y) bisect the line joining [tex]A(x_1,y_1)](https://img.qammunity.org/2020/formulas/mathematics/high-school/9oamcqyst81dnvauqvfcqehaidawvwsfvw.png) and
and
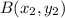 internally
internally
Now from the attached image we can guess the values of
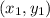 and
and
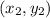 and the values of m and n are 3 and 2 respectively
and the values of m and n are 3 and 2 respectively
Substituting the values and simplifying we get
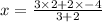
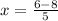
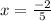
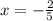
Now solving for y coordinate
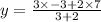
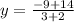
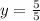
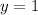
Hence the coordinates of point p which divides the line BA in ration 3:2 will be