Question

PLEASE HELP AND ANSWER!!!!! Which of the following reveals the minimum value for the equation 2x2 + 12x − 14 = 0?

2(x + 6)2 = 26
2(x + 6)2 = 20
2(x + 3)2 = 32
2(x + 3)2 = 30

Answer 1

2(x + 3)^2 = 32

Explanation:

The "COMPLETING THE SQUARE" lesson makes it clear that this is the correct answer.

(I just took the test)

Answer 2

The correct option is 3.

Explanation:

The given equation is

`2x^2+12x-14=0`

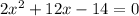
It can be written as

`(2x^2+12x)-14=0`

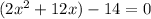
Taking out the common factor form the parenthesis.

`2(x^2+6x)-14=0`

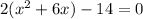
If an expression is defined as
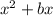`x^2+bx` then we add
`((b)/(2))^2` to make it perfect square.

In the above equation b=6.

Add and subtract 3^2 in the parenthesis.

`2(x^2+6x+3^2-3^2)-14=0`

`2(x^2+6x+3^2)-2(3^2)-14=0`

`2(x+3)^2-18-14=0`

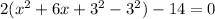
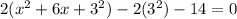
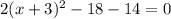
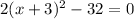`2(x+3)^2-32=0` .... (1)

Add 32 on both sides.

`2(x+3)^2=32`

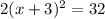
The vertex from of a parabola is

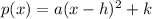`p(x)=a(x-h)^2+k` .... (2)

If a>0, then k is minimum value at x=h.

From (1) and (2) in is clear that a=2, h=-3 and k=-32. It means the minimum value is -32 at x=-3.

The equation
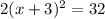`2(x+3)^2=32` reveals the minimum value for the given equation.

Therefore the correct option is 3.