Question

Which values of x and y would make the following expression represent a real number? (4+5i)(x+yi)

Answer 1

So x=4 and y=-5 would work.

Explanation:

When you multiply complex conjugates, you get a real result.

Example:

`(a+bi)(a-bi)=a^2-b^2i^2=a^2+b^2`

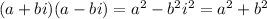
I replace
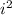`i^2` with -1 since
`i^2=-1`.

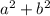`a^2+b^2` is a real number (there is no imaginary part, no i).

So what is the conjugate of 4+5i?

4-5i

So x=4 and y=-5 would work.

A multiple of the complex conjugate would work as well.

`(a+bi)(ca-cbi)`

`c(a+bi)(a-bi)`

`c(a^2-b^2i^2)`

`c(a^2+b^2)`

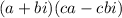
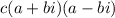
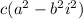
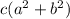
This is still a real number; there is no imaginary part,no i.