Question

A billiard ball moving at 6.00 m/s strikes a stationary ball of the same mass. After the collision, the first ball moves at 5.12 m/s at an angle of 31.5° with respect to the original line of motion. Assuming an elastic collision (and ignoring friction and rotational motion), find the struck ball's velocity after the collision. magnitude m/s direction ° counter-clockwise from the original direction of motion

Answer 1

Magnitude : 3.14 m/s

Direction : 301.31 deg

Step-by-step explanation:

Assuming that the ball moves in positive x-direction initially.

`m` = mass of each ball

`\underset{v_(1i)}{\rightarrow}` = initial velocity of first ball before collision =
`6\hat{i} + 0\hat{j}`

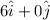
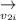`\underset{v_(2i)}{\rightarrow}` = initial velocity of second ball before collision =
`0\hat{i} + 0\hat{j}`

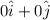
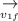`\underset{v_(1f)}{\rightarrow}` = final velocity of first ball after collision =
`5.12 Cos31.5\hat{i} + 5.12 Sin31.5\hat{j}`

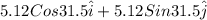
`\underset{v_(2f)}{\rightarrow}` = final velocity of second ball after collision = ?

Using conservation of momentum

`m`
`\underset{v_(1i)}{\rightarrow}` +
`m`
`\underset{v_(2i)}{\rightarrow}` =
`m`
`\underset{v_(1f)}{\rightarrow}` +
`m`
`\underset{v_(2f)}{\rightarrow}`

(
`6\hat{i} + 0\hat{j}`) + (
`0\hat{i} + 0\hat{j}`) = (
`5.12 Cos31.5\hat{i} + 5.12 Sin31.5\hat{j}`) +
`\underset{v_(2f)}{\rightarrow}`

`\underset{v_(2f)}{\rightarrow}` = (
`6\hat{i} + 0\hat{j}`) - (
`5.12 Cos31.5\hat{i} + 5.12 Sin31.5\hat{j}`)

`\underset{v_(2f)}{\rightarrow}` =
`1.63\hat{i} - 2.68\hat{j}`

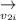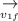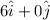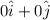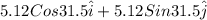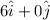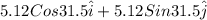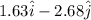
magnitude of final velocity of second ball is given as

magnitude = sqrt((1.63)² + (- 2.68)²) = 3.14 m/s

Direction is given as

θ = 360 + tan⁻¹(- 2.68/1.63)

θ = 301.31 deg