Question

A wire is made from a material having a temperature coefficient of resistivity of 0.0003125 (°C^-1). In an experiment, we maintain a constant potential difference of 150 volts across the wire and measure the power dissipation in it as a function of temperature ; at a temperature of 20° C, the power dissipation is 300 watts. What is the (%) change in the power dissipation as the wire's temperature rises from 20°C to 1820°C?

Answer 1

The percentage change in the power dissipation as the wire's temperature rises from 20°C to 1820°C is 36%.

Step-by-step explanation:

Given that,

Temperature coefficient of resistivity = 0.0003125

Potential difference = 150 V

Temperature = 20° C

Power = 300 watt

Wire's initial temperature = 20°C

Wire's final temperature = 1820°C

We need to calculate the resistance at 20°C

Using formula of power

`P=(V^2)/(R_(0))`

`R_(0)=(V^2)/(P)`

Where, P = power

V = Potential difference

`R_(0)=(150^2)/(300)`

`R_(0)=75\ \Omega`

We need to calculate the resistance at 1820°C

Using formula of temperature of coefficient of resistivity

`R=R_(0)(1+\alpha(T-T_(0)))`

`R=75(1+0.0003125(1820-20))`

`R=117.19\ \Omega`

We need to calculate the power

Using formula of power

`P'=(V^2)/(R)`

`P'=(150^2)/(117.19)`

`P'=192\ Watt`

We need to calculate the percentage change in the power dissipation as the wire's temperature rises from 20°C to 1820°C

`\Delta P=|(P'-P)/(P)|*100`

`\Delta P=|(192-300)/(300)|*100`

`\Delta P=36\%`

Hence, The percentage change in the power dissipation as the wire's temperature rises from 20°C to 1820°C is 36%.

Answer 2

The power decreases by 36%

Step-by-step explanation:

Given:

At 20° C

Power, P₀ = 300 W

Potential difference, V = 150 volts

Now, power is given as

P = V²/R

where, R is the resistance

on substituting the values, we get

300 = 150²/R₀

or

R₀ = 75 Ω

Now, the variation of resistance with temperature is given as

R = R₀[1 + α(T - T₀)]

where, α is the temperature coefficient of resistivity = 0.0003125 (°C⁻¹)

now, at

T₀ = 20° C

R₀ = 75 Ω

for

T = 1820° C

we have

R = R₀[1 + α(T - T₀)]

substituting the values

we get

R = 75×[1 + 0.0003125 × (1820 - 20)]

or

R = 117.18 Ω

Now using the formula for power

We have,

P = V²/R

or

P = 150²/117.18 = 192 W

Therefore, the percentage change will be

=
`(P-P_0)/(P_0)* 100`

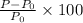
on substituting the values , we get

=
`(192-300)/(300)* 100`

= -36%

here, negative sign depicts the decrease in power