Question

Could someone please help me with this? Assume that the half-life of ^14C is 6000 years. State the estimated age of a sample of mummified skin from a prehistoric human that contained 6.25 percent of an original quantity of ^14C.

Answer 1

Given:

half life of
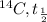`^(14)C , t_{(1)/(2)}` = 6000 years

%quantity contained in sample,
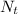`N_(t)` = 6.25%
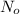`N_(o)` original quantity = 0.0625
`N_(o)`

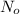
Formula used:

Formula for carbon dating is given by:

`t = (\ln (N)/(N_(o)))/(-0.693).t_{(1)/(2)}`

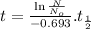
where,

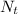`N_(t)` = amount of radio active material

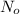`N_(o)` = amount of original material

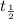`t_{(1)/(2)}` = half life

Solution:

Using the formula mentioned above with suitable values given:

`t = (\ln (0.0625N_(o))/(N_(o)))/(-0.693)* 6000`

`t = (\ln 0.0625)/(-0.693)* 6000`

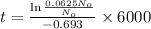
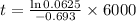
t = 24005.097 years

Therefore, the estimated age of the sample of the mummified skin is 24005.097 years