Question

As a hiker in Glacier National Park, you are looking for a way to keep the bears from getting at your supply of food. You find a campground that is near an outcropping of ice from one of the glaciers. Part of the ice outcropping forms a 55.5 ° slope up to a vertical cliff. You decide that this is an ideal place to hang your food supply as the cliff is too tall for a bear to reach it. You put all of your food into a burlap sack, tie an unstretchable rope to the sack, and tie another bag full of rocks to the other end of the rope to act as an anchor. You currently have 22.5 kg of food left for the rest of your trip so you put 22.5 kg of rocks in the anchor bag to balance it out. What happens when you lower the food bag over the edge and let go of the anchor bag? The weight of the bags and the rope are negligible. The ice is smooth enough to be considered frictionless.What will be the acceleration of the bags when you let go of the anchor bag?

Answer 1

Acceleration of the bags is 0.861 m/s²

Step-by-step explanation:

Given:

Mass of the rock, m = 22.5 kg = mass of the food

Slope, Θ = 55.5°

Now, from the figure, we have

T - mgsinΘ = ma ...................(1)

'a' is the acceleration of the mass

where T is the tension

also for the second mass, we have

mg - T = ma

now substituting the value of T from the equation (1) we get

mg - (ma + mgsinΘ) = ma

or

mg(1 - sinΘ) = (m + m)a

or

a =
`(mg(1 - sin\theta))/(2m)`

on substituting the values we get

a =
`(9.8* (1 - sin55.5^o))/(2)`

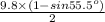
or

a = 0.861 m/s²

Hence, the acceleration of the bags is 0.861 m/s²