Question

If the tension in a string is doubled, then a natural frequency will (a) increase, (b) decrease by ________?

Answer 1

(a) increase by
`√(2)` times

Step-by-step explanation:

Natural frequency of a wave in a string is given by:

`f = (1)/(2L)\sqrt{(T)/(\mu)}`

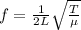
where, L is the length of the string, T is the tension in the string and
`\mu` is the linear density of the string.

Considering the length and linear density of the string are constant, if the tension in a string is doubled, the natural frequency of the string would:

`f\propto √(T)`

`(f_n)/(f)=\sqrt{(T_n)/(T)}\\ \Rightarrow f_n =\sqrt{(2T)/(T)}f = √(2) f`

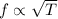
Thus, the natural frequency of the string would increase by
`√(2)` times.