Question

A 16.0-m uniform ladder weighing 480 N rests against a frictionless wall. The ladder makes a 55.0° angle with the horizontal. (a) Find the horizontal and vertical forces the ground exerts on the base of the ladder when an 850-N firefighter has climbed 3.80 m along the ladder from the bottom.

(b) If the ladder is just on the verge of slipping when the firefighter is 9.40 m from the bottom, what is the coefficient of static friction between ladder and ground?

Answer 1

horizontal force component 535.00 N

vertical force component 1330 N

`\mu= 0.38`

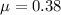
Step-by-step explanation:

from equilibrium condition at A

`N_2(16 sin55) = 850*(3.80cos55) +480((16)/(2)cos55)`

`N_2(13.12) = 535.00 N`

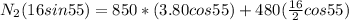
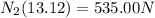
FROM equilibrium condition

N_1 = mg +850

= 480 + 850

= 1330 N

horizontal force component

f_2 = N_2

= 535.00 N

vertical force component

N_1 = 1330 N

B) Coefficient of friction between ladder and ground when fire fighter is 9.4 m away from ground

`N_2(16 sin55) = 850*(9.40cos55) +480((16)/(2)cos55)`

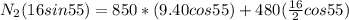
N_2 =517.71 N

Thus coefficient of friction is

`\mu = (f_2)/(N_1)`

=
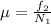
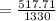`= (517.71)/(1330)` [f_2 = N_2]

= 0.38