Answer:
(a) 3.0 μF
(b) 75.0 μF
Step-by-step explanation:
The equivalent capacitance when the capacitors are connected all in series is:
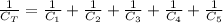
Where
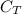 is the equivalent capacitance,
is the equivalent capacitance,
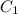 ,
,
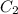 ,
,
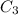 ,
,
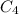 and
and
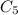 are the capacitance of each capacitors. In this case, they all have 15.0 μF. So we can replace as:
are the capacitance of each capacitors. In this case, they all have 15.0 μF. So we can replace as:
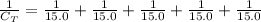
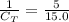
The solve for
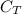 :
:
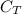 =3.0 μF
=3.0 μF
The equivalent capacitance when the capacitors are connected all in parallel is:
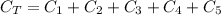
Replacing values we get:
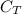 =15.0 μF+15.0 μF+15.0 μF+15.0 μF+15.0 μF
=15.0 μF+15.0 μF+15.0 μF+15.0 μF+15.0 μF
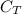 =75.0 μF
=75.0 μF