Question

The length of one leg of a right triangle is 3 feet more than the other leg. If the hypotenuse is 15 feet find the length of each leg

Answer 1

One leg = x = 9.

Other leg = x+3 = 9+3 = 12.

Explanation:

We have given hypotenuse = 15 feet and one leg is more than other the other of a right triangle.

We need to find the each leg of the right triangle.

Let the one leg = x.

Let the other leg = x+3.

We know that, Pythagoras theorem:

`Hypotenuse^(2) = Perpendicular^(2) + Base^(2)`

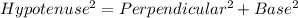
Hypotenuse = 15, one leg(base) = x and other leg(perpendicular) = x+3.

By applying pythagoras theorem:

`15^(2) = x^(2) + ( x+3)^(2)`

225 = x^{2} + x^{2} + 9 +6x

225 = 2x^{2} + 6x + 9

Subtracting 9 from both sides

216 = 2x^{2} + 6x

2x^{2} + 6x -216 = 0

Taking 2 common,

x^{2} + 3x - 108 = 0

x^{2} + 12x - 9x - 108 = 0

x(x+12) - 9(x+12) = 0

(x+12) (x-9)

x = -12, x = 9.

So, we will consider positive value x = 9.

Therefore, one leg = x = 9.

Other leg = x+3 = 9+3 = 12.

Answer 2

Leg1 = 9 and leg2 = 12

Explanation:

Points to remember

Pythagorean theorem

Hypotenuse² = Base² + Height²

To find the length of each leg

It is given that, hypotenuse = 15 feet

Let base = x the height = x +3

By using Pythagorean theorem we can write,

Hypotenuse² = Base² + Height²

15² = x² + (x + 3)²

225 = x² + x² + 6x + 9

2x² + 6x + 216 = 0

x² + 3x + 108 = 0

By solving we get x = 9 and x -12

Therefore one leg = 9 and other leg = 9 + 3 = 12