Answer:
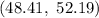
Step-by-step explanation:
The confidence interval for population mean is given by :-
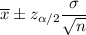
Given : Sample size :
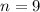
Sample mean :
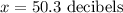
Standard deviation :

Significance level :

Critical value :
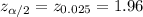
Now, the 95% confidence interval estimate of the (true, unknown) mean sound intensity of all food processors of this type :-
