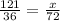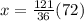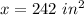Question

The area of rectangle ABCD is 72 square inches. A diagonal of rectangle ABCD is 12 inches and the diagonal of rectangle EFGH is 22 inches. Find the area of rectangle EFGH. Round to the nearest square inch if necessary.

Answer 1

The area of rectangle EFGH is
`242\ in^(2)`

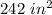
Explanation:

For this problem I assume that rectangle ABCD and rectangle EFGH are similar

step 1

Find the scale factor

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional, and this ratio is called the scale factor

Let

z ------> the scale factor

The scale factor is the ratio between the diagonals of rectangles

so

`z=(22)/(12)=(11)/(6)`

step 2

Find the area of rectangle EFGH

we know that

If two figures are similar, then the ratio of its areas is the scale factor squared

Let

z------> the scale factor

x -----> area of rectangle EFGH

y ----> area of rectangle ABCD

so

`z^(2)=(x)/(y)`

we have

`z=(11)/(6)`

`y=72\ in^(2)`

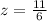
substitute and solve for x

`((11)/(6))^(2)=(x)/(72)`

`(121)/(36)=(x)/(72)`

`x=(121)/(36)(72)`

`x=242\ in^(2)`