Question

The combustion of 1 L of gasoline releases about 3.4×10^7J of energy. In one car's engine, about 80% of that energy is lost as heat. a. How much work is done by the engine for each liter of gasoline burned? (answer in MJ/L)

b. If the car requires 5.9×10^5 J of work to travel 1 km, find the fuel efficiency in km/L.

Answer 1

A) The work done by the engine is: 6.8MJ/L

B) The fuel efficiency is
`11.53{(km)/(L)`

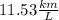
Step-by-step explanation:

A)

We know that the gasoline releases about 3.4*10^7 J of energy for each liter, and about 80% of that energy is lost as heat; it means that the other 20% of the energy released is taken for the engine to do work. In that sense, the work done by the engine is 20% of the 3.4*10^7 J that the gasoline releases for 1 liter, so:

`W_E=3.4*10^7J*(20)/(100)=6.8*10^6J =6.8MJ`

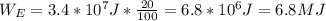
This last can be seen as a conversion factor, where we multiply the energy released by the gasoline by the factor (20 J taken for do work for each 100 J released).

B) We know that the car requires 5.9*10^5 J of work for each km traveled. That is the energy that the car requires, but it is not the energy that you have to give to the car; take in mind that the energy that you put in the car in gasoline liters will be not taken all, but just 20%. Also we know that the work done by the engine for 1 liter of gasoline is 6.8MJ, and that is just the work taken for do work (the useful energy), so we can connect both data:

`{(1km)/(5.9*10^5J)*(6.8*10^6J)/(1L)=11.53(km)/(L)`

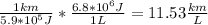
The first fraction,
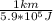`(1km)/(5.9*10^5J)` is the ratio or the proportion of (1 km requieres 5.9*10^5 J); and we multiply by the second fraction
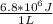`(6.8*10^6J)/(1L)`, which is the ratio: 6.8*10^6 J of work done for each liter of gasoline.