Question

One and one-half moles of an ideal monatomic gas expand adiabatically, performing 7900 J of work in the process. What is the change in temperature of the gas during this expansion?

Answer 1

The temperature change is -633.15K

Step-by-step explanation:

If we considered the expansion as a reversible one (to be adiabatic is one of the requirements), the work done by expansion can be written as:

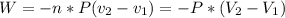`W=-n*P(v_2-v_1)=-P*(V_2-V_1)` Where 2 and 1 subscripts mean the final and the initial state respectively. The equation negative sign says that for an expansion of the gas, the system is making work, so the energy is going out of the system.

Using the ideal gas equation, it is possible to change volume and pressure by temperatures:

`PV_2=(nRT_2)\\PV_1=nRT_1`

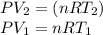
So,

`W=-nR(T_2-T_1)`

`(T_2-T_1)=(-W)/(nR)=(-7900J)/((1.5mol*8.314(J)/(molK)))=-633.5K`

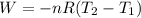
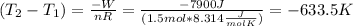
This result makes sense considering that the volume increases, so it is expected that the temperature decreases.