Answer:
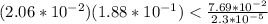
Explanation:
Verify each statement
Part 1) we have
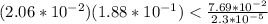
Solve the left side
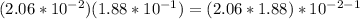
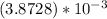
Solve the right side
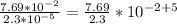
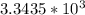
substitute in the inequality
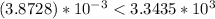
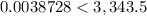 -----> is true
-----> is true
therefore
The statement is correct
Part 2) we have
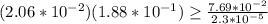
Solve the left side
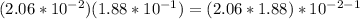
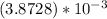
Solve the right side
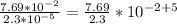
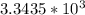
substitute in the inequality
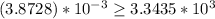
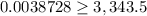 -----> is not true
-----> is not true
therefore
The statement is not correct
Part 3) we have
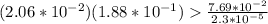
Solve the left side
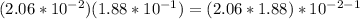
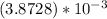
Solve the right side
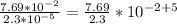
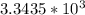
substitute in the inequality
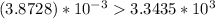
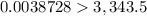 -----> is not true
-----> is not true
therefore
The statement is not correct
Part 4) we have
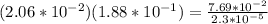
Solve the left side
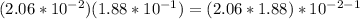
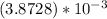
Solve the right side
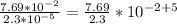
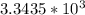
substitute in the equation
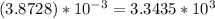
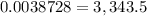 -----> is not true
-----> is not true
therefore
The statement is not correct