Answer:
+/- 1,
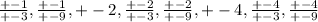 ....
....
Explanation:
The Rational root theorem states that If f(x) is a Polynomial with integer coefficients and if there exist a rational root of the form p/q then p is the factor of the constant term of the function and q is the factor of the leading coefficient of the function
Given: f(x)= 9x^4-2x^2-3x+4
Factors of q (leading coefficient) are: +/-9, +/-3, +/-1
Factors of p (constant term) are: +/-4 , +/-2, +/- 1
According to the theorem we write the roots in p/q form:
Therefore,
p/q =+/- 1,
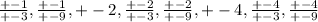 ....
....