Question

In △ABC,a=14, b=17, and c=22. Find m∠A

Answer 1

∠A = 39.52°

Explanation:

In Δ ABC,

a = 14, b = 17 and c = 22 then we have to find the measure of ∠A.

Since a² = b² + c² - 2.b.c.cosA [ From cosine law]

(14)² = (17)²+ (22)² - 2(17)(22)cosA

196 = 289 + 484 - (748)cosA

196 = 773 - (748)cosA

748(cosA) = 773 - 196 = 577

cosA =
`(577)/(748)=0.7714`

A =
`cos^(-1)(0.7714)`

A = 39.52°

Answer 2

m∠A = 39.5°

Explanation:

* Lets revise how to find the measure of an angle by using the cosine rule

- In any triangle ABC

# ∠A is opposite to side a

# ∠B is opposite to side b

# ∠C is opposite to side c

- The cosine rule is:

# a² = b² + c² - 2bc × cos(A)

# b² = a² + c² - 2ac × cos(B)

# c² = a² + b² - 2ab × cos(C)

- To find the angles use this rule

# m∠A =
`cos^(-1)(b^(2)+c^(2)-a^(2))/(2bc)`

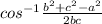
# m∠B =
`cos^(-1)(a^(2)+c^(2)-b^(2))/(2ac)`

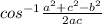
# m∠C =
`cos^(-1)(a^(2)+b^(2)-c^(2))/(2ab)`

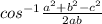
* Lets solve the problem

∵ a = 14 , b = 17 , c = 22

∵ m∠A =
`cos^(-1)(b^(2)+c^(2)-a^(2))/(2bc)`

∴ m∠A =
`cos^(-1)(17^(2)+22^(2)-14^(2))/(2(17)(22))`

∴ m∠A =
`cos^(-1)(289+484-196)/(748)`

∴ m∠A =
`cos^(-1)(577)/(748)`

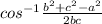
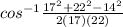
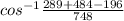
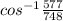
∴ m∠A = 39.5°