Question

According to the Rational Root Theorem, which statement about f(x) = 66x4 – 2x3 + 11x2 + 35 is true? Any rational root of f(x) is a factor of 35 divided by a factor of 66. Any rational root of f(x) is a multiple of 35 divided by a multiple of 66. Any rational root of f(x) is a factor of 66 divided by a factor of 35. Any rational root of f(x) is a multiple of 66 divided by a multiple of 35.

Answer 1

A

Explanation:

trust bro

Answer 2

The correct option is Any rational root of f(x) is a factor of 35 divided by a factor of 66....

Explanation:

According to the rational root theorem:

if
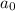`a_(0)` and
`a_(n)` are non zero then each rational solution x will be:

x= +/- Factors of
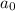`a_(0)` / Factors of
`a_(n)`

In the given polynomial we have:

66x4 – 2x3 + 11x2 + 35

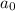`a_(0)` = 35

`a_(n)` = 66

Therefore,

x= +/- Factors of 35/ Factors of 66.

Thus the correct option is Any rational root of f(x) is a factor of 35 divided by a factor of 66....