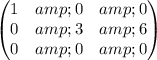Question

Find the reduced echelon form of [1, 2, 4; 0, 3, 6; 0, 2, 4]

Answer 1

`\begin{pmatrix}1&0&0\\0&3&6\\0&0&0 \end{pmatrix}`

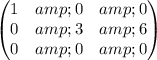
Explanation:

Given:

`\begin{pmatrix}1&2&4\\0&3&6\\0&2&4 \end{pmatrix}`

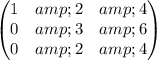
We need to reduce the given matrix to reduced echelon form.

Solution:

Make zeroes in column 1 except the entry at row 1, column 1. As we can see all elements in column are already zero. Make zeroes in column 2 except the entry at row 2, column 2.

`\begin{pmatrix}1&2&4\\0&3&6\\0&2&4 \end{pmatrix}\\R_3\rightarrow R_3-(2)/(3)R_2\\\begin{pmatrix}1&2&4\\0&3&6\\0&0&0 \end{pmatrix}\\R_2\rightarrow (R_2)/(3)\\\begin{pmatrix}1&2&4\\0&1&2\\0&0&0 \end{pmatrix}\\R_1\rightarrow R_1-2R_2\\\begin{pmatrix}1&0&0\\0&3&6\\0&0&0 \end{pmatrix}\\`

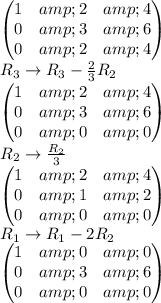
So,
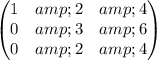`\begin{pmatrix}1&2&4\\0&3&6\\0&2&4 \end{pmatrix}` in reduce echelon form is
`\begin{pmatrix}1&0&0\\0&3&6\\0&0&0 \end{pmatrix}`