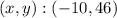2 Answers

Pihu · Answer 1 · 2020-12-01T18:35:49+0000

For this case we must indicate the solution of the following system of equations:

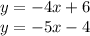
$y = -4x + 6\\y = -5x-4$

Equating both equations we have:

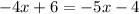
-4x + 6 = -5x-4

Adding 5x to both sides of the equation:

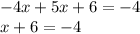
$-4x + 5x + 6 = -4\\x + 6 = -4$

Subtracting 6 from both sides of the equation:

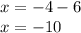
$x = -4-6\\x = -10$

We look for the value of y:

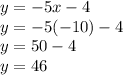
$y = -5x-4\\y = -5 (-10) -4\\y = 50-4\\y = 46$

Thus, the solution is:
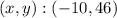
(x, y): (- 10,46)

Answer:

Please log in or register to add a comment.