Answer:
Solution is

Explanation:
Given Differential Equation,
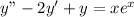 ...............(1)
...............(1)
We need to solve the given differential equations using undetermined coefficients.
Let the solution of the given differential equation is made up of two parts. one complimentary solution and one is particular solution.
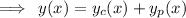
For Complimentary solution,
Auxiliary equation is as follows
m² - 2m + 1 = 0
( m - 1 )² = 0
m = 1 , 1
So,
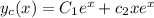
Now for particular solution,
let
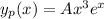


Now putting these values in (1), we get
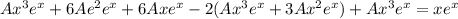

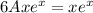
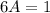
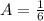

Therefore, Solution is
