Answer:
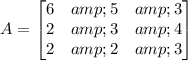
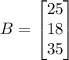
Explanation:
It is given that the snack shop makes 3 mixes of nuts in the following proportions.
Mix I: 6 lbs peanuts, 2 lbs cashews, 2 lbs pecans.
Mix II: 5 lbs peanuts, 3 lbs cashews, 2 lbs pecans.
Mix III: 3 lbs peanuts, 4 lbs cashews, 3 lbs pecans.
they received an order for 25 of mix I, 18 of mix II, and 35 of mix III.
We need to find the matrices A & B for which AB gives the total number of lbs of each nut required to fill the order.
Mix I Mix II Mix III
peanuts 6 5 3
cashews 2 3 4
pecans 2 2 2
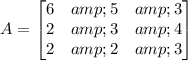
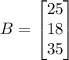
The product of both matrices is
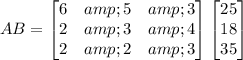
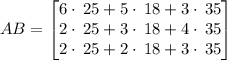
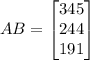
Therefore matrix AB gives the total number of lbs of each nut required to fill the order.