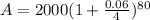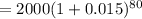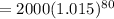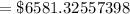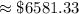Question

Find the future value of $2,000 deposited into a retirement account, after 20 years, if the interest rate is 6%, compounded quarterly. (Use the formula for this problem) $_____

Answer 1

$ 6581.33 ( approx )

Explanation:

Since, future value formula in compound interest is,

`A=P(1+(r)/(n))^(nt)`

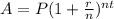
Where,

P = Principal amount,

r = annual rate,

n = number of compounding periods in a year,

t = number of years,

Here, P = $ 2,000, r = 6% = 0.06, n = 4 ( 1 year = 4 quarters ),

t = 20 years,

Hence, the future value would be,

`A=2000(1+(0.06)/(4))^(80)`

`=2000(1+0.015)^(80)`

`=2000(1.015)^(80)`

`=\$ 6581.32557398`

`\approx \$ 6581.33`