Question

Y1=x^4 is a solutionto the ode x^2y"-7xy'+16y=0 use reduction of order to find another independant solution

Answer 1

`y_2=x^4lnx`

Explanation:

We are given that a differential equation

`x^2y''-7xy'+16y=0`

And one solution is
`y_1=x^4`

We have to find the other independent solution by using reduction order method

`y''-(7)/(x)y'+(16)/(x^2)y=0`

Compare with the equation

`y''+P(x)y'+Q(x)y=0`

Then we get P(x)=
`-(7)/(x)['/tex] Q(x)=[tex](16)/(x^2)`

`y_2=y_1\int(e^(-\intP(x)dx))/(y^2_1)dx`

`y_2=x^4\int\frac{e^{(7)/(x)}dx}}{x^8}dx`

`y_2=x^4\int(e^(7ln x))/(x^8)dx`

`y_2=x^4\int(x^7)/(x^8)dx`

`e^(xlny)=y^x`

`y_2=x^4\int frac{1}{x}dx`

`y_2=x^4lnx`

Answer 2

Answer with explanation:

The given differential equation is

x²y" -7 x y' +1 6 y=0---------(1)

Let, y'=z

y"=z'

`(dy)/(dx)=z\\\\y=zx`

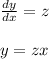
Substitution the value of y, y' and y" in equation (1)

→x²z' -7 x z+16 zx=0

→x² z' + 9 zx=0

→x (x z'+9 z)=0

→x=0 ∧ x z'+9 z=0

`x (dz)/(dx)+9 z=0\\\\(dz)/(z)=-9 (dx)/(x)\\\\ \text{Integrating both sides}\\\\ \log z=-9 \log x+\log K\\\\ \log z+\log x^9=\log K\\\\\log zx^9=\log K\\\\K=zx^9\\\\K=y'x^9\\\\K x^(-9)d x=dy\\\\\text{Integrating both sides}\\\\y=(-K)/(8x^8)+m`

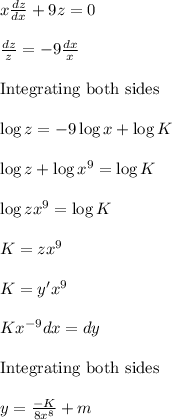
is another independent solution.where m and K are constant of integration.