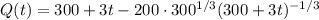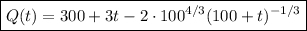Question

A tank holds 300 gallons of water and 100 pounds of salt. A saline solution with concentration 1 lb salt/gal is added at a rate of 4 gal/min. Simultaneously, the tank is emptying at a rate of 1 gal/min. Find the specific solution Q(t) for the quantity of salt in the tank at a given time t.

Answer 1

The amount of salt in the tank changes with rate according to

`Q'(t)=\left(1(\rm lb)/(\rm gal)\right)\left(4(\rm gal)/(\rm min)\right)-\left((Q(t))/(300+(4-1)t)(\rm lb)/(\rm gal)\right)\left(1(\rm gal)/(\rm min)\right)`

`\implies Q'+\frac Q{300+3t}=4`

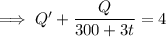
which is a linear ODE in
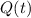`Q(t)`. Multiplying both sides by
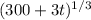`(300+3t)^(1/3)` gives

`(300+3t)^(1/3)Q'+(300+3t)^(-2/3)Q=4(300+3t)^(1/3)`

so that the left side condenses into the derivative of a product,

`\big((300+3t)^(1/3)Q\big)'=4(300+3t)^(1/3)`

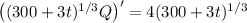
Integrate both sides and solve for
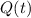`Q(t)` to get

`(300+3t)^(1/3)Q=(300+3t)^(4/3)+C`

`\implies Q(t)=300+3t+C(300+3t)^(-1/3)`

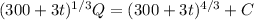
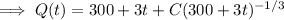
Given that
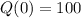`Q(0)=100`, we find

`100=300+C\cdot300^(-1/3)\implies C=-200\cdot300^(1/3)`

and we get the particular solution

`Q(t)=300+3t-200\cdot300^(1/3)(300+3t)^(-1/3)`

`\boxed{Q(t)=300+3t-2\cdot100^(4/3)(100+t)^(-1/3)}`