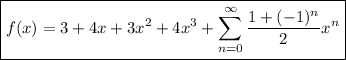The generating function for this sequence is
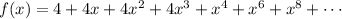
assuming the sequence itself is {4, 4, 4, 4, 1, 0, 1, 0, ...} and the 1-0 pattern repeats forever (as opposes to, say four 4s appearing after every four 1-0 pairs). We can make this simpler by "displacing" the odd-degree terms and considering instead the generating function,

where the coefficients of
 follow a much more obvious pattern of alternating 1s and 0s. Let
follow a much more obvious pattern of alternating 1s and 0s. Let
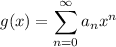
where
 is recursively given by
is recursively given by
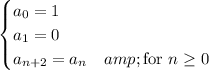
and explicitly by
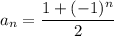
so that
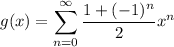
and so