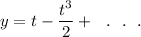Answer: The required solution is
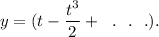
Step-by-step explanation: We are given to find the solution of the following differential equation using power series method :

Let
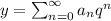 be the solution of the given equation.
be the solution of the given equation.
Then, we have
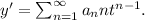
From equation (i), we get
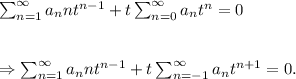
Comparing the coefficients of
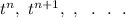 from both sides of the above, we get
from both sides of the above, we get
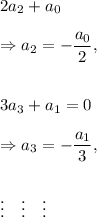
Therefore, we get

The condition y(0) = 1 gives
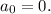
So, the required solution is