Question

1. Consider the equation ax^2+bx+c=0, where a, b and c are odd integers. Prove that if z is a solution to the given equation, then z must be an irrational number. You may assume that sum of two odd integers is even product of two odd integers is odd sum of two even integers is even product of two even integers is even sum of an odd and an even integer is odd product of an odd and an even integer is even

Answer 1

Explanation:

Given that

`ax^2+bx+c=0`

Where a,b,and c are odd integers.

We know that solution of quadratic equation given by following formula

`z=(-b\pm √(b^2-4ac))/(2a)`

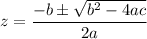
Now we have to prove that above solution is a irrational number when a,b and c all are odd numbers.

Let's take a=3 ,b=9 ,c= -3 these are all odd numbers.

Now put the values

`z=(-9\pm √(9^2-4* 3* (-3)))/(2* 3)`

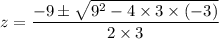
So

`z=(-9\pm √(117))/(6)`

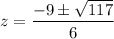
We know that square roots,cube roots etc are irrational number .So we can say that above value z is also a irrational number.

When we will put any values of a,b and c (they must be odd integers) oue solution will be always irrational.