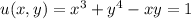Explanation:
The given equation is
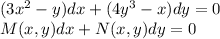
As a check for exactness we have
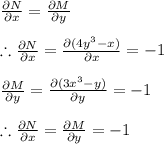
Hence the given equation is an exact differential equation and thus the solution is given by
thus the solution is given by

Similarly we have

Comparing both the solutions we infer
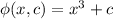
Hence the solution becomes
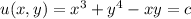
given boundary condition is that it passes through (1,1) hence
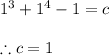
thus solution is