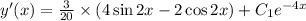Question

Solve the inhomogeneius linear ode by undetermined coefficients
Y"+4y=3sin2x

Answer 1

Answer with explanation:

The given non Homogeneous linear differential equation is:

y" +4 y'=3 Sin 2 x-------(1)

Put , u=y'

Differentiating once

u'=y"

Substituting the value of , y' and y" in equation (1)

⇒u' +4u =3 Sin 2x

This is a type of linear differential equation.

Integrating factor
`=e^(4t)`

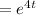
Multiplying both sides of equation by Integrating factor

`e^(4 x)(u'+4u)=e^(4x)3 \sin 2x\\\\ \text{Integrating both sides}\\\\ue^(4x)=\int {3 \sin 2x * e^(4x)} \, dx \\\\ue^(4x)=(3e^(4x))/(2^2+4^2)* (4\sin 2x -2 \cos 2x)\\\\ue^(4x)=(3e^(4x))/(20)* (4\sin 2x -2 \cos 2x)+C_(1)\\\\ \text{Using the formula of}\\\\\int{e^(ax)\sin bx } \, dx=(e^(ax))/(a^2+b^2)* (a \sin bx-b \cos bx)+C`

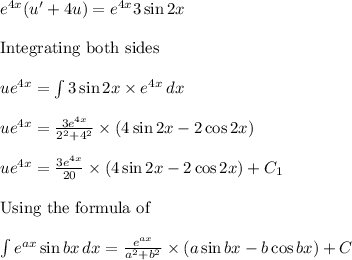
where C and
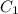`C_(1)` are constant of integration.

Replacing , u by , y' in above equation we get the solution of above non homogeneous differential equation

`y'(x)=(3)/(20)* (4\sin 2x -2 \cos 2x)+C_(1)e^(-4 x)`