We have
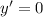 when
when
 or
or
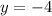 , so we need to check the sign of
, so we need to check the sign of
 on 3 intervals:
on 3 intervals:
- Suppose
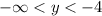 . In particular, let
. In particular, let
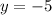 . Then
. Then
 . Since
. Since
 is negative on this interval, we have
is negative on this interval, we have
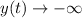 as
as
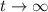 .
. - Suppose
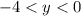 , say
, say
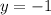 . Then
. Then
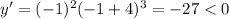 , so that
, so that
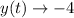 as
as
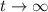 .
. - Suppose
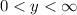 , say
, say
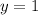 . Then
. Then
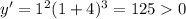 , so that
, so that
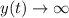 as
as
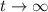 .
.
We can summarize this behavior as in the attached plot. The arrows on the
 -axis indicate the direction of the solution as
-axis indicate the direction of the solution as
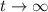 . We then classify the solutions as follows.
. We then classify the solutions as follows.
 is an unstable solution because on either side of
is an unstable solution because on either side of
 ,
,
 does not converge to the same value from both sides.
does not converge to the same value from both sides.
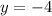 is a semi-stable solution because for
is a semi-stable solution because for
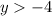 , solutions tend toward the line
, solutions tend toward the line
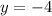 , while for
, while for
 solutions diverge to negative infinity.
solutions diverge to negative infinity.