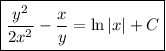Question

Find an implicit solution to the ODE. ("Homogeneous") y' = y^2x/y^3 +x^3 + y/x

Answer 1

I'm going to guess that you meant to include parentheses somewhere, so that the ODE is supposed to be

`y'=(y^2x)/(y^3+x^3)+\frac yx`

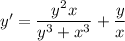
Then substitute
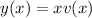`y(x)=xv(x)` so that
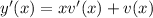`y'(x)=xv'(x)+v(x)`. Then

`xv'+v=(x^3v^2)/(x^3v^3+x^3)+v`

`xv'=(v^2)/(v^3+1)`

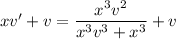
which is separable as

`(v^3+1)/(v^2)\,\mathrm dv=\frac{\mathrm dx}x`

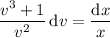
Integrate both sides: on the left,

`\displaystyle\int(v^3+1)/(v^2)\,\mathrm dv=\int\left(v+\frac1{v^2}\right)\,\mathrm dv=\frac12v^2-\frac1v`

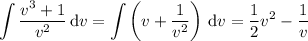
The other side is trivial. We end up with

`\frac12v^2-\frac1v=\ln|x|+C`

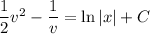
Solve in terms of
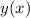`y(x)`:

`\boxedx`