Answer:
17,101,185, 269,.... is the solution.
i.e. x≡17 mod(84) is the solution
Explanation:
Given that the system is
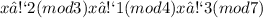
Considering from the last as 7 is big,
possible solutions would be 10,17,24,...
Since this should also be 1(mod4) we get this as 1,5,9,...17, ...
Together possible solutions would be 17, 45,73,121,....
Now consider I equation and then possible solutions are
5,8,11,14,17,20,23,26,29,...,47,....75, ....
Hence solution is 17.
Next number satisfying this would be 101, 185, ...