Question

Find the least squares approximation of the the data (0, 1), (1, 2), (2, 1/2) (3, 3) using the quadratic function p(x) = a_0 + a_1 x + a_2 x^2. Plot p(x) along with the data to compare.

Answer 1

The required function is
`p\left(x\right)=1.325-0.675x+0.375x^2`.

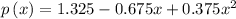Explanation:

The given data points are (0, 1), (1, 2), (2, 1/2) and (3, 3).

Let the quadratic function is defined as

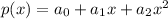`p(x)=a_0+a_1x+a_2x^2` .... (1)

Using graphing calculator, we get

`a_0=1.325`

`a_1=-0.675`

`a_2=0.375`

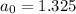
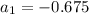
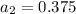
Substitute
`a_0=1.325`,
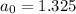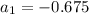`a_1=-0.675` and
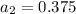`a_2=0.375` in function (1), to find the quadratic function.

`p\left(x\right)=1.325-0.675x+0.375x^2`

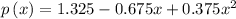
Therefore the required function is
`p\left(x\right)=1.325-0.675x+0.375x^2`.

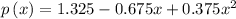The graph of data points and quadratic function is shown below.