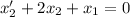Answer:
a.
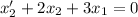
b.
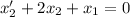
Explanation:
We are given differential equation of second order in each part
We have to change given differential equation into first order differential equation
a.y''+2y'+3y=0
Suppose
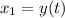
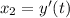
Differentiate w.r.t times then we get
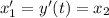
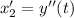
Substitute the values in the given differential equation then we get
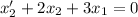
b.y''+2y'+y=0
Suppose
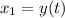
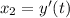
Differentiate w.r.t time
Then we get
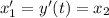
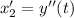
Substitute the values in given differential equation