Question

Use induction to prove the following formula is true for all integers n where n greaterthanorequalto 1. 1 + 4 + 9 + .. + n^2 = n(n + 1)(2n + 1)/6

Answer 1

Answer with Step-by-step explanation:

Since we have given that

1+4+9+........................+n² =
`(n(n+1)(2n+1))/(6)`

We will show it using induction on n:

Let n = 1

L.H.S. :1 = R.H.S. :
`(1* 2* 3)/(6)=(6)/(6)=1`

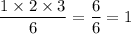
So, P(n) is true for n = 1

Now, we suppose that P(n) is true for n = k.

`1+4+9+...................+k^2=(k(k+1)(2k+1))/(6)`

Now, we will show that P(n) is true for n = k+1.

So, it L.H.S. becomes,

`1+4+9+......................+(k+1)^2`

and R.H.S. becomes,

`((k+1)(k+2)(2k+3))/(6)`

Consider, L.H.S.,

`1+4+9+..+k^2+(k+1)^2\\\\=(k(k+1)(2k+1))/(6)+(k+1)^2\\\\=k+1[(k(2k+1))/(6)+(k+1)]\\\\=(k+1)[(2k^2+k+6k+6)/(6)]\\\\=(k+1)(2k^2+7k+6)/(6)]\\\\=(k+1)(2k^2+4k+3k+6)/(6)]\\\\=(k+1)[(2k(k+2)+3(k+2))/(6)]\\\\=((k+1)(2k+3)(k+2))/(6)`

So, L.H.S. = R.H.S.

Hence, P(n) is true for all integers n.