Question

A sequence of three real numbers forms an arithmetic progression with a first term of 9. If 2 is added to the second term and 20 is added to the third term, the three resulting numbers form a geometric progression. What is the smallest possible value for the third term of the geometric progression?

Answer 1

The smallest possible value for the third term of the geometric progression is 1.

Explanation:

Given : A sequence of three real numbers forms an arithmetic progression with a first term of 9. If 2 is added to the second term and 20 is added to the third term, the three resulting numbers form a geometric progression.

To find : What is the smallest possible value for the third term of the geometric progression?

Solution :

The arithmetic progression is given by
`a,a+d,a+2d`

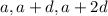
First term a=9

Second term - 2 is added to second term i.e.
`a+d+2=9+d+2=11+d`

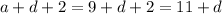
Third term - 20 is added to the third term i.e.
`a+2d+20=9+2d+20=29+2d`

The geometric progression is given by
`a,ar,ar^2`

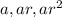
First term a=9

Second term -
`ar=11+d`

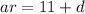
Third term
`ar^2=29+2d`

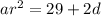
r is the common ratio which is second term divided by first term,

So,
`r=(ar)/(a)=(11+d)/(9)`

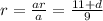
or third term divided by second term,

So,
`r=(ar^2)/(ar)=(29+2d)/(11+d)`

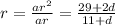
Equating both the r,

`(11+d)/(9)=(29+2d)/(11+d)`

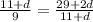
Cross multiply,

`(11+d)* (11+d)=(29+2d)(9)`

`11^2+11d+11d+d^2=261+18d`

`121+22d+d^2-261-18d=0`

`d^2+4d-140=0`

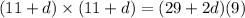
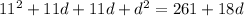
Solving by middle term split,

`d^2+14d-10d-140=0`

`d(d+14)-10(d+14)=0`

`(d+14)(d-10)=0`

`d=-14,10`

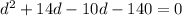
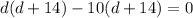
Substituting the value of d in the third term,

Third term
`ar^2=29+2d`

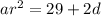
When d=-14,

Third term
`ar^2=29+2(-14)=29-28=1`

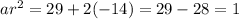
When d=10,

Third term
`ar^2=29+2(10)=29+20=49`

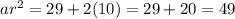
Therefore, The smallest possible value for the third term of the geometric progression is 1.