Answer:
c = 13.2
Explanation:
* Lets explain how to solve the problem
- In Δ ABC
# Side a is opposite to ∠A
# Side b is opposite to ∠B
# Side c is opposite to ∠C
- The sine rule is:
#

* Lets solve the problem
- In Δ ABC
∵ m∠A = 16°
∵ m∠B = 49°
∵ The sum of the measures of the interior angles of a triangle is 180°
∴ m∠A + m∠B + m∠C = 180°
∴ 16° + 49° + m∠C = 180°
∴ 65° + m∠C = 180° ⇒ subtract 65° from both sides
∴ m∠C = 115°
- Lets use the sine rule to find c
∵ a = 4 and m∠A = 16°
∵ m∠C = 115°
∵
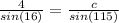
- By using cross multiplication
∴ c sin(16) = 4 sin(115) ⇒ divide both sides by sin(16)
∴
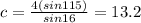
* c = 13.2