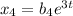Question

Find the real-valued general solution to the system x' = (-1 -2 4 3)x

Answer 1

The real-valued general solution to the system is:

`x=\left[\begin{array}{ccc}x_1\\x_2\\x_3\\x_4\end{array}\right]=\left[\begin{array}{ccc}b_1e^(-t)\\b_2e^(-2t)\\b_3e^(4t)\\b_4e^(3t)\end{array}\right]`

Explanation:

We are given a system as:

`x'=(-1\ \ -2\ \ 4\ \ 3)x`

i.e.

we have:

`\left[\begin{array}{ccc}x_1'\\x_2'\\x_3'\\x_4'\end{array}\right]=[-1\ \ -2\ \ 4\ \ 3]\left[\begin{array}{ccc}x_1\\x_2\\x_3\\x_4\end{array}\right]`

i.e.

`\left[\begin{array}{ccc}x_1'\\x_2'\\x_3'\\x_4'\end{array}\right]=\left[\begin{array}{ccc}-x_1\\-2x_2\\4x_3\\3x_4\end{array}\right]`

Let the variables x_i's be differentiated with respect to t.

i.e. we have:

`x_1'=-x_1\\\\i.e.\\\\(x_1')/(x_1)=-1`

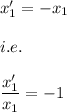
on integrating both side of the equation we have:

`\log x_1=-t+c_1\\\\i.e.\\\\x_1=e^(-t+c_1)\\\\i.e.\\\\x_1=e^(-t)e^(c_1)\\\\i.e.\\\\x_1=b_1e^(-t)`

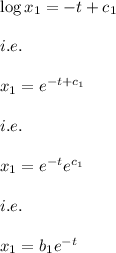
Similarly,

`x_2'=-2x_2\\\\i.e.\\\\(x_2')/(x_2)=-2\\\\\\\text{on\ integrating\ both\ side}\\\\\log x_2=-2t+c_2\\\\i.e.\\\\x_2=b_2e^(-2t)`

Similarly we get:

`x_3=b_3e^(4t)`

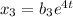
and

`x_4=b_4e^(3t)`