Answer:
HCF(91,39) = 13 and HCF(73,21) = 1
Explanation:
As per euclidian algorithm, a = bq + r, where a is dividend, b is divisor, q is quotient and r is remainder.
We can use euclidian algorithm to find the HCF of numbers.
To find: HCF ( 91, 39 ):
On dividing 91 by 39, we get
91=39×2+13
Here, remainder = 13
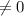
So, again applying division algorithm on 39 and 13, we get
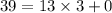
As remainder = 0 and divisor at this step is equal to 13, HCF = 13 .
To find: HCF ( 73, 21 )
On dividing 73 by 21, we get
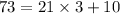
Here, remainder = 10
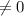
On applying division algorithm on 21 and 10, we get
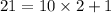
Here, remainder = 1
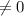
On applying division algorithm on 10 and 1, we get
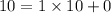
As remainder = 0 and divisor at this step is 1, HCF = 1