Solution:
The given differential equation is
x y" -(x+n)y'+ny=0------------(1)
Let, y'=t
y"=t'
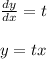
Substituting the value of , y', y'' and y in equation (1)
→x t' -(x+n)t+n t x=0
→ x t' = x t+ n t- nt x
→ x t'=t(x+n-nx)

which is a solution of Differential equation.
(b)

Integrating both sides
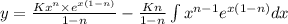
required linear independent solution of Differential equation.