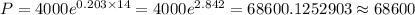Question

During a research​ experiment, it was found that the number of bacteria in a culture grew at a rate proportional to its size. At 1010​:00 AM there were 4 comma 0004,000 bacteria present in the culture. At​ noon, the number of bacteria grew to 4 comma 6004,600. How many bacteria will there be at​ midnight?

Answer 1

68600 will there be at​ midnight ( approx )

Explanation:

Let P shows the population of the bacteria,

Since, the number of bacteria in a culture grew at a rate proportional to its size,

`\implies (dP)/(dt)\propto P`

`(dP)/(dt)=kP`

Where, k is the constant of proportionality,

`(dP)/(P)=kdt`

`\int (dP)/(P)=\int kdt`

`ln P=kt + C_1`

`P=e^(kt+C_1)`

`P=e^(kt).e^(C_1)=C e^(kt)`

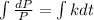
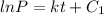
Now, let the population of bacteria is estimated from 10:00 AM,

So, at t = 0, P = 4,000 ( given )

`4000 = Ce^(0)`

`\implies C=4000`

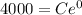
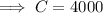
Now, at noon there are 4,600 bacterias,

That is, at t = 2, P = 4600

`4600=Ce^(2k)`

`4600 = 4000 e^(2k)`

`\implies e^(2k)=(4600)/(4000)=1.15`

`2k=ln(1.5)\implies k=(ln(1.5))/(2)=0.202732554054\approx 0.203`

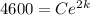
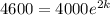
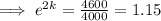
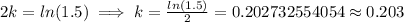
Hence, the equation that represents the population of bacteria after t hours,

`P=4000 e^(0.203t)`

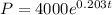
Therefore, the population of the bacteria at midnight ( after 14 hours ),

`P=4000 e^(0.203* 14)=4000 e^(2.842)= 68600.1252903\approx 68600`