Question

What is the shortest-wavelength x-ray radiation in m that can be generated in an x-ray tube with an applied voltage of 93.3 kV? m (b) Calculate the photon energy in eV eV (c) Explain the relationship of the photon energy to the applied voltage. The maximum photon energy is just the applied voltage times the electron charge. The value of the voltage in volts equals the value of the maximum photon energy in electron volts. The maximum photon energy is just the applied voltage times the electron charge. The value of the voltage in volts equals the inverse of the value of the maximum photon energy in electron volts. The maximum photon energy is just the applied voltage divided by the electron charge. The value of the voltage in volts equals the value of the maximum photon energy in electron volts. The maximum photon energy is just the applied voltage divided by the electron charge. The value of the voltage in volts equals the inverse of the value of the maximum photon energy in electron volts.

Answer 1

(a)
`1.33\cdot 10^(-11) m`

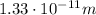
The x-rays in the tube are emitted as a result of the collisions of electrons (accelerated through the potential difference applied) on the metal target. Therefore, all the energy of the accelerated electron is converted into energy of the emitted photon:

`e \Delta V = (hc)/(\lambda)`

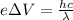
where the term on the left is the electric potential energy given by the electron, and the term on the right is the energy of the emitted photon, and where:

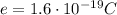`e=1.6\cdot 10^(-19)C` is the electron's charge

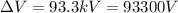`\Delta V = 93.3 kV = 93300 V` is the potential difference

`h=6.63\cdot 10^(-34) Js` is the Planck constant

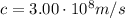`c=3.00\cdot 10^8 m/s` is the speed of light

`\lambda` is the wavelength of the emitted photon

Solving the formula for
`\lambda`, we find:

`\lambda=(hc)/(e\Delta V)=((6.63\cdot 10^(-34))(3\cdot 10^8))/((1.6\cdot 10^(-19))(93300))=1.33\cdot 10^(-11) m`

(b) 93300 eV (93.3 keV)

The energy of the emitted photon is given by:

`E=(hc)/(\lambda)`

where

h is Planck constant

c is the speed of light

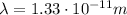`\lambda=1.33\cdot 10^(-11) m` is the wavelength of the photon, calculated previously

Substituting,

`E=((6.63\cdot 10^(-34))(3\cdot 10^8))/(1.33\cdot 10^(-11))=1.50\cdot 10^(-14) J`

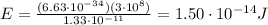
Now if we want to convert into electronvolts, we have to divide by the charge of the electron:

`E=(1.50\cdot 10^(-14) J)/(1.6\cdot 10^(-19) J/eV)=93300 eV`

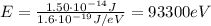
(c) The following statements are correct:

The maximum photon energy is just the applied voltage times the electron charge. (1)

The value of the voltage in volts equals the value of the maximum photon energy in electron volts.

In fact, we see that statement (1) corresponds to the equation that we wrote in part (a):

`e \Delta V = (hc)/(\lambda)`

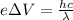
While statement (2) is also true, since in part (b) we found that the photon energy is 93.3 keV, while the voltage was 93.3 kV.