Question

Formulate the situation as a system of inequalities. (Let x represent the number of dinghies the company can manufacture and y represent the number of rowboats.)

A boat company manufactures aluminum dinghies and rowboats. The hours of metal work and painting needed for each are shown in the table, together with the hours of skilled labor available for each task. How many of each kind of boat can the company manufacture?

(hours) Dinghy Rowboat Labor Available
Metal Work 2 3 120
Painting 2 2 90
leftbrace6.gif
(labor for metal work)
(labor for painting)
x ? 0, y ? 0

Sketch the feasible region.


Find the vertices. (Order your answers from smallest to largest x, then from smallest to largest y.)

(x, y) =
leftparen1.gif
rightparen1.gif
(x, y) =
leftparen1.gif
rightparen1.gif
(x, y) =
leftparen1.gif
rightparen1.gif
(x, y) =
leftparen1.gif
rightparen1.gif

Answer 1

x (smallest to largest) = 0,45 ,55

y (smallest to largest) = 0,10,40

Explanation:

(hours) Dinghy Rowboat Labor Available

Metal Work 2 3 120

Painting 2 2 110

Let x represent the number of dinghies the company can manufacture and y represent the number of rowboats.

So, total hours for metal work =
`2x+3y`

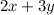
So, total hours for Painting =
`2x+2y`

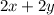
So, equation becomes:

`2x+3y\leq 120`

`2x+2y\leq 110`

`x\geq 0`

`y\geq 0`

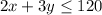
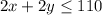
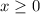
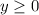
Plot the inequalities

Refer the attached figure

So, the vertices of the feasible region are (0,40),(45,10) and (55,0)

So, x values are 0 , 45 and 55

x represents the number of dinghies

So, x (smallest to largest) = 0,45 ,55

y values are 40,10,0

y represent the number of rowboats.

So, y (smallest to largest) = 0,10,40