Question

If S is countable and nonempty, prove their exist a surjection g: N --> S

Math: Analysis and Proof

Answer 1

Answer with Step-by-step explanation:

We are given S be any set which is countable and nonempty.

We have to prove that their exist a surjection g:N
`\rightarrow S`

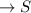
Surjection: It is also called onto function .When cardinality of domain set is greater than or equal to cardinality of range set then the function is onto

Cardinality of natural numbers set =
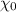`\chi_0`( Aleph naught)

There are two cases

1.S is finite nonempty set

2.S is countably infinite set

1.When S is finite set and nonempty set

Then cardinality of set S is any constant number which is less than the cardinality of set of natura number

Therefore, their exist a surjection from N to S.

2.When S is countably infinite set and cardinality with aleph naught

Then cardinality of set S is equal to cardinality of set of natural .Therefore, their exist a surjection from N to S.

Hence, proved