Question

According to a​ study, 73.6% of college freshmen majoring in business said that​ "to get training for a specific​ career" was a very important reason for their going to college. Consider a group of six freshman business majors selected at random. Find the probability that no more than two of the six freshmen in the group felt that this reason was very important.

Answer 1

Answer: 4.54%

Explanation:

The binomial probability formula :-

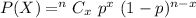`P(X)=^nC_x \ p^x\ (1-p)^(n-x)`, where P(x) is the probability of getting success in x trials, n is total number of trials and p is the probability of getting succes in each trial.

Given : The proportion of college freshmen majoring in business said that​ "to get training for a specific​ career" was a very important reason for their going to college :
`p=0.736`

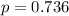
Now, if six freshman business majors selected at random, then the probability that no more than two of the six freshmen in the group felt that this reason was very important. :-

`P(x\leq2)=P(0)+P(1)+P(2)\\\\=^6C_0 \ (0.736)^0\ (1-0.736)^(6)+^6C_1 \ (0.736)^1\ (1-0.736)^(5)+^6C_2 \ (0.736)^2\ (1-0.736)^(4)\\\\=(0.264)^6+6(0.736)(0.264)^5+15(0.736)^2(0.264)^4\\\\=0.04547116664\approx0.0454=4.54\%`

Hence, the probability that no more than two of the six freshmen in the group felt that this reason was very important= 4.54 %