Answer:
The value of k is 18.
Explanation:
Here, the AP is,

Let a be the first term and d is the common difference,
So the arithmetic sequence would be,

Given,
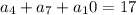
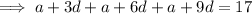

Now,
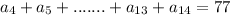
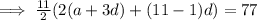
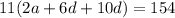
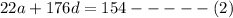
22 × equation (1) - 3 × equation (2),
We get,
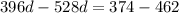
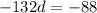

From equation (1),
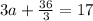
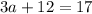
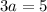
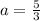
Here,
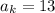
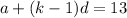
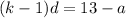
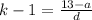
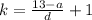
By substituting the value,
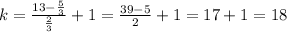
Hence, the value of k is 18.