Question

1.prove that the following three functions are linearly dependent

f1=x^2; f2(x)=1-x^2; f3=2+x^2

Answer 1

Proof:

Given any functions
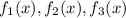`f_(1)(x),f_(2)(x),f_(3)(x)` they are linearly dependent if we can find values of
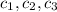`c_(1),c_(2),c_(3)` such that

`c_(1)f_(1)(x)+c_2f_(2)(x)+c_(3)f_(3)(x)=0`

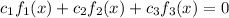
Using the given functions in the above equation we get

`c_(1)f_(1)(x)+c_2f_(2)(x)+c_(3)f_(3)(x)=0\\\\c_(1)x^(2)+c_(2)(1-x^(2))+c_(3)(2+x^(2))=0\\\\\Rightarrow (c_(1)-c_(2)+c_(3))x^(2)+c_(1)+c_(2)+2c_(3)=0`

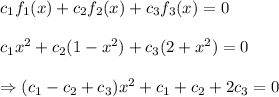
This will be satisfied if and only if

`c_1-c_2+c_3=0,c_1+c_2+2c_3=0`

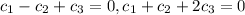
Solving the equations we get

`c_1+2c_3=-c_2\\\\c_1+c_1+2c_3+c_3=0\\2c_1+3c_3=0`

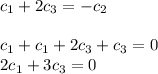
Since we have 3 variables and 2 equations thus we will get many solutions

one being if we put
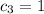`c_3=1` we get

`c_1+2c_3=-c_2\\\\c_1+c_1+2c_3+c_3=0\\2c_1+3c_3=0\\\\c_1=(-3)/(2)\\\\c_2=(-1)/(2)`

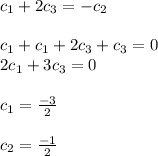
Thus we have
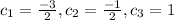`c_1=(-3)/(2),c_2=(-1)/(2),c_3=1` as one solution. Hence the given functions are linearly dependent.